Bittiefe ist neben Dynamikumfang und Abtastrate ein Begriff über den jeder Musiker grundlegend Bescheid wissen sollte. Sei es, um kryptische Bezeichnungen an digitalen Effektgeräten besser einordnen zu können oder, um zu verstehen, wie Signalverarbeitung in modernen DAWs funktioniert. Was die Bittiefe (Samplingtiefe) aussagt und warum sie großen Einfluss auf die Qualität deiner Aufnahmen haben kann wirst du in diesem Beitrag erfahren.
Ein grundlegendes Verständnis von Bittiefe ist immer dann vorteilhaft, wenn Dynamik aus der analogen in die digitale Domäne übertragen werden soll. In der analogen Welt wird die Amplitude eines Signales anhand von elektrischen Spannungswerten beschrieben. Das ermöglicht eine stufenlose Abbildung mit unendlich vielen Abstufungen. In der digitalen Domäne hingengen, müssen diese unendlich vielen Analogwerte in ein vorgegebenes Raster eingepasst werden. Nur so können sie später digital verarbeitet und interpretiert werden. Die Samplingtiefe gibt dabei an, wie viele mögliche Werte an einem Abtastpunkt (Sample) zur Beschreibung der Amplitude zur Verfügung stehen.
1. Bittiefe (Samplingtiefe)
Das Wort Bit ist ein Kofferwort aus den englischen Wörtern „binary“ und „digit“. Es wird in der Digitaltechnik entweder als Maßeinheit für den Informationsgehalt oder als Maßeinehit für die Datenmenge verwendet. Als Einheit für die Datenmenge kommt es zum Beispiel bei Dateneraten (Bitrate) von Mp3-Dateien oder bei Übertragungsraten von Netzwerken vor. Diese werden in kbps (kilo bits per second) angegeben – also in tausenden Bits pro Sekunde. Für die Musikproduktion ist das Bit als Ausdruck für den möglichen Informationsgehalt (Informationstiefe) eines Abtastpunktes aber viel wichtiger. Diese Angabe findest du zum Beispiel bei der Audio-CD (16 Bit), beim Aufnehmen (24 Bit) und während der Bearbeitung (32 oder 64 Bit Gleitkomma-Werte) von Musik.
1.1 Vom Bit zur Bittiefe
Bei der Auswahl einer passenden Bittiefe für deine Aufnahmen solltest du beachten, dass sich zu geringe Samplingtiefen negativ auf die Qualität deiner aufgenommenen Signale auswirken können. Warum das so ist, kann am einfachsten anhand einer Exponentialfunktione mit der Basis zwei erklärt werden. Das klingt erstmal kompliziert, ist es aber nicht! Folgende Beispiele sollten dabei etwas Licht ins Dunkel bringen:
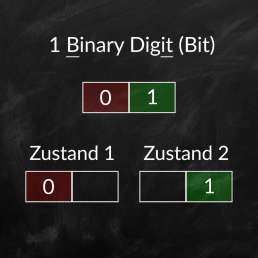
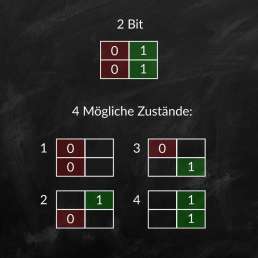
Wenn das Bit als Maßeinheit für den Informationsgehalt verwendet wird, dann enthält ein Bit den Informationsgehalt von zwei gleich wahrscheinlichen Möglichkeiten. Dabei kann die enthaltene Information entweder „null“ oder „eins“ sein. Umgelegt auf die Musikproduktion würde also eine Bittiefe von einem Bit die Abbildung von zwei möglichen Zuständen für die Amplitude zulassen.
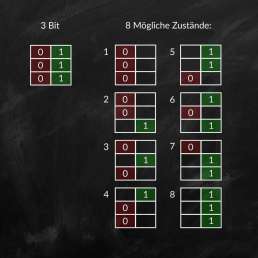
Wird die Anzahl der Bits auf drei erhöht, können schon acht mögliche Zustände abgebildet werden. Das entspricht einer Samplingtiefe von 3-Bit. Dabei nähern wir uns jetzt schön langsam Bittiefen, die bei der Wiedergabe schon ansatzweise erahnen lassen wie das gespeicherte Signal ursprünglich geklungen hat.
Mit jedem zusätzlichen Bit wird die Auflösung pro Abtastpunkt weiter erhöht. Die möglichen Zustände pro Bittiefe folgen dabei der vohin erwähnten Exponentialfunktion mit Basis zwei. Diese lautet wie folgt: Die möglichen Zustände pro Bit (Basis = 2) hoch der Anzahl der vorhandenen Bits (Exponent = 1, 2, 4, 8, 16, 24, …) ergiebt die maximal möglichen Zustände der jeweiligen Bittiefe.
1.2 Bittiefe in der Musikproduktion
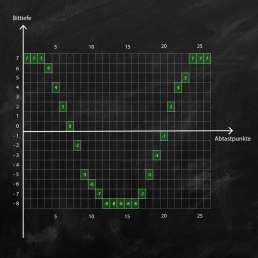
Wenn in der Musikproduktion von einer Bittiefe von 16-Bit die Rede ist, dann entspricht das 65536 möglichen Zuständen. Diese stehen für die Speicherung des Dynamikumfanges (Amplitude) zur Verfügung – 32767 Möglichkeiten für die positive- und 32768 Möglichkeiten für die negative Halbwelle. Zur Veranschaulichung hier ein kurzes, stark vereinfachtes Beispiel einer Signalabtastung mit einer Samplingtiefe von 4-Bit (ohne Speicherung von Vorzeichen):
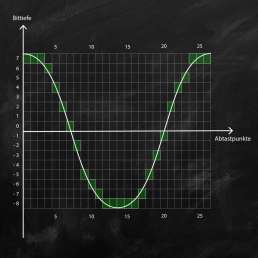
Abgetastet wird eine Sinusschwingung mit einer Bittiefe von 4-Bit. Das entspricht 16 Möglichkeiten zur Speicherung der Amplitude. Für die positive und negative Halbwelle stehen jeweils 8 Werte zur Verfügung, wobei bei den positiven Werten auch der Wert „0“ inkludiert ist. Dieser Wert entspricht dem Ruhezustand der Membran eines Lautsprechers.
Nach der Abtastung ist bei jedem Abtastpunkt ein Amplitudenwert zwischen +7 und -8 gespeichert. Anhand dieser Werte kann das Signal später wieder rekonstruiert werden. Bei einer Wiedergabe muss dieses Signal aber aufgrund der geringen Samplingtiefe von 4-Bit einen hohen Detailverlust hinnehmen. Es kann nicht mehr originalgetreu wiedergegeben werden und würde stark verzerrt klingen.
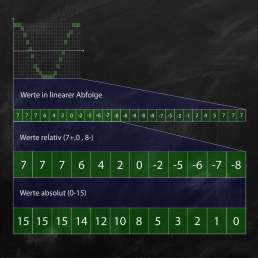
Die Amplitudenwerte werden z.B. in einer PCM-Datei in linearer Abfolge gespeichert. Bie einer Bittiefe von 4-Bit müssen sie von 16 relativen Werten (+7 bis -8) in 16 absolute Werte (0-15) umgewandelt werden – Vorzeichen können/sollen ja nicht gespeichert werden. So können sie später als Maschinencode vom Prozessor deines Rechners ausgelesen werden.
Die absoluten Werte werden als Binärcode in einem sogenannten Integer Datentyp gespeichert. Dieser kann im Gegensatz zu Gleitkomma-Datentypen (z.B. Float) nur ganzzahlige Werte speichern. In unserem Beispiel kann ein 4-Bit Integer den Wert „0“ als kleinsten (Binär: 0000) und den Wert 15 als höchsten Wert (Binär: 1111) abspeichern.
1.3 Vorteil von hohen Bittiefen
Wie die vorherigen beiden Beispiele hoffentlich veranschaulichen konnten, verdoppelt sich die Auflösung des Dynamikbereichs mit jedem zusätzlichen Bit. Wenn also die Samplingtiefe von 16-Bit auf 24-Bit erhöht wird stehen 8 Bit (!) mehr zur Speicherung der Dynamik zur Verfügung. Das entspricht einer Erhöhung der Auflösung um das 255-fache. Eine Auflösung von 24-Bit ist also schon ziemlich allen Anforderungen gewachsen. Für dich bedeutet das: nutze immer die höchste Bittiefe, die dein Equipment verarbeiten kann! So verschenkst du kein unnötiges Potential und höhere Bittiefen machen fast immer mehr Sinn als höhere Abtastraten.
1.4 Dynamikumfang und Bittiefe
Vergleicht man die Bittiefe mit dem Dynamikumfang in Dezibel (dB), ergibt sich eine einfache Formel: Pro zusätzlichem Bit erhöht sich der abbildbare Dynamikumfang um 6 dB. Das bedeutet, dass eine Audio CD mit 16-Bit einen theoretischen Dynamikumfang von 96 dB abbilden kann. Eine Tonaufnahme mit 24-Bit kann hingegen schon einen theoretischen Dynamikumfang von 144 dB abbilden – ein Drittel mehr als die Audio CD. Der theoretische Dynamibereich wird dabei aber durch das sogenannte Grundrauschen und durch das Verzerrungsverhalten von elektronischen Bauteilen eingeschränkt.
1.4 Gleitkommawerte
Wenn du Signale mit einer Bittiefe von 24-Bit aufnimmst, stehen dir 16 777 216 mögliche Werte zur Abbildung der Dynamik zur Verfügung. Das klingt nach enorm viel. Was du aber bedenken musst ist, dass bei der Bearbeitung in der DAW eine ganze Menge Signale mit jeweils 16 777 216 möglichen Werten viele male addiert und subtrahiert werden. Dabei kann es zu einem Überlauf der verwendeten ganzzahligen Integer Datentypen kommen.
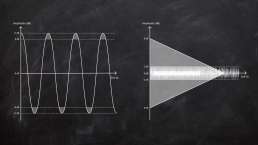
Für diesen Fall werden interne Berechnungen in den meisten DAWs mit sogenannten Gleitkomma-Datentypen (z.B. 32-Bit Float) ausgeführt. Ein 32-Bit Float Datentyp hat z.B. zusätzlich zu den 24-Bit zur Speicherung ganzzahliger Werte noch weitere 8 Bit für die Berechung von Überläufen zur Verfügung. Somit ergibt sich bei einer Samplingtiefe von 32 Bit ein theoretischer Dynamikumfang von über 1600 dB – Übersteuerungen sind somit in der DAW eigentlich nicht mehr möglich!
Fazit
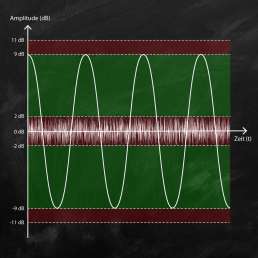
Die Wahl der richtigen Bittiefe kann entscheidenden Einfluss auf die Qualität deiner Aufnahme haben. Aus diesem Grund solltest in jedem Produktionsschritt immer die höchstmögliche Bittiefe verwenden. Bei der Verwendung von 32-Bit Gleitkommawerten kannst du die Pegelanzeigen in der DAW auch mal rot aufleuchten lassen, ohne gleich in Panik verfallen zu müssen. Versichere dich nur, dass an deinem Stereo Ausgang (Master Bus) alles wieder im grünen Bereich ist.
Wenn du mehr Fragen zum Thema Recording hast, kannst du gerne in meinen Homerecording Beiträgen nach Antworten stöbern.
Beitragsbild: Chris Hörmann
Quellen: Wikipedia (2019)
Interessante Bücher und Videos
Ähnliche Beiträge
Der Dynamikumfang (Dynamikbereich) in der Tontechnik
Der Dynamikumfang (Dynamikbereich) ist neben der Abtastrate (Sample Rate) einer der technisch…
Wie funktioniert Analog-Digital-Wandlung bzw. Digital-Analog-Wandlung?
Im modernen Homestudio ist Digitaltechnik, und vor allem digitale Signalverarbeitung, fast überall…
Abtastrate / Samplerate / Samplingfrequenz – Begriffserklärung
Der Begriff Abtastrate (auch Samplerate oder Samplingfrequenz) ist ein technischer Fachausdruck aus…










Hallo lieber Chris Hoermann- habe Deinen Bericht mit Intresse gelesen. Herzlichen Dank. Was mmir noch unklar ist, ist der Dynamikumfang bei 32 Bit. Oben beschreibst du, dass pro Bit 6dB dazu kommen. Dann kämen zu den 144dB noch 8 mal 6db dazu, was bei 32 Bit 192dB wären und niicht 1600dB. Auf das gleiche Resultat komme ich, wenn ich 20 mal den Logaritmus von 2hoch 32 nehme.
Wo mach ich einen Überlegungsfehler?
Mit freundlichen Grüssen
Ivo
Hallo Ivo,
ich müsste mich da auch wieder genauer reinlesen warum genau 1600 db, aber es hat damit zu tun, dass bei 32Bit der Datentyp Float – also ein Datentype mit Dezimalstellen – verwendet wird. Genauer gesagt kommen zu den 24 Bit noch 8 Bit dazu, mit denen die Nachkommastellen abgebildet werden können. Es kann also damit eigentlich kein digitales Clipping geben, da die Übersteuerungen mit den 8 Bit im Nachkommabereich abgebildet werden können. Ich hoffe das bringt mal etwas Licht ins Dunkel.